Turbo Pascal - 8 ферзей на доске

Ферзь - самая сильная фигура в шахматах. Это объясняется тем, что возможности для ходов и атаки объединяют возможности всех остальных фигур кроме коня. Таким образом, ферзь может ходить как прямо, так и по диагонали на любое количество клеток. Под его контролем находится более 20 позиций одновременно. Не попасть под удар этой фигуры очень сложно. Одной из самых популярных шахматных задач - это задача о 8 ферзях.

Задача о 8 ферзях

Цель задачи - расставить 8 ферзей на доске так, чтобы они не били друг друга. Эта задача была придумана Максом Беццелем еще в 1848 году. Только спустя несколько лет были представлены всевозможные решения. А их конечность и вовсе доказана в 1874 году английским математиком Глешшером.

Согласно теории определителей задача "8 ферзей" имеет 92 способа решения, двенадцать из которых основные, а остальные являются лишь их симметричным отражением по той или иной оси, либо достигаются поворотом шахматной доски. Существуют решения, когда фигуры не занимают главную диагональ и не находятся на одной прямой.

Решение задачи 8 ферзей

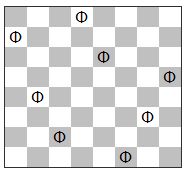
8 ферзей в Pascal

В среде Turbo Pascal 8 ферзей расставить на доске можно используя так называемые эвристические алгоритмы. Метод перебора с отходом назад является наиболее универсальным. Для решения задачи 8 ферзей на Паскаль необходимо организовать двумерный массив 8x8, который будет представлять собой шахматную доску. Так как два ферзя не могут стоять на одной строке и в одном столбце, то все значения первого или второго индекса элемента будут различными. Общее число переборов будет равняться 8!=40320.

Скачать:

8 ферзей - Возможность выбора решения задачи 8 ферзей в Паскале методом перебора

Задача о 8 ферзях - Метод перебора с отходом назад