Метод Гаусса. Решение систем уравнений методом Гаусса.

Метод Гаусса является наиболее оптимальным и быстрым решением систем линейный уравнений (СЛУ). По сути методом Гаусса мы решали системы уравнений еще в школе, не зная его названия. Ранее он был известен как метод последовательного исключения переменных из уравнений. Метод Гаусса имеет несколько вариаций, с помощью него можно решать не только СЛУ, но и вычислять обратную матрицу, находить определитель (детерминант матрицы), вычислять значение интеграла. Рассмотрим по порядку все вариации метода Гаусса с подробным разбором примеров.

Решение системы уравнений методом Гаусса

Все методы решения систем уравнений делятся на: точные и приближенные. Метод Гаусса является точным решением систем уравнений, так как последовательность действий при нахождении корней конечно, приближенные методы считаются иттерационно, т.е до тех пор, пока погрешность вычислений не будет меньше заданной.

Основной идеей метода Гаусса,как и отмечалось ранее, является последовательное исключение неизвестных, приводящее к построению эквивалентной системы с треугольной матрицей. Рассмотрим следующую систему уравнений 4 порядка:

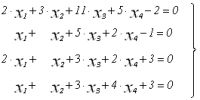
Метод Гаусса при решении системы уравнений можно разделить на два этапа: прямой и обратный ход. Вычисление неизвестных ведется в обратной последовательности: x₄,x₃ x₂,x₁. Необходимым и достаточным условием выполнения метода Гаусса должно быть следующим: все ведущие элементы А_ii не должны равняться нулю.

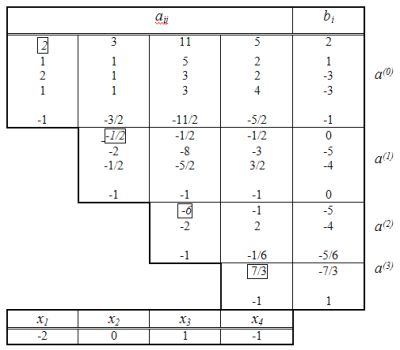
Решение системы уравнений методом Гаусса в табличном представлении (bi- свободные члены) .

Прямой ход:

Ведущий элемент А₁₁=2.

Нормирование первого уравнения: x₁=-(3/2)*x₂-(11/2)*x₃-(5/2)*x₄+1.

Исключение неизвестной x₁ из оставшихся трех уравнений:

2-е уравнение: (-(3/2)*1+1)*x₂+(-(11/2)*1+5)*x₃+(-(5/2)*1+2)*x₄+(1*1-1)=0

3-е уравнение: (-(3/2)*2+1)*x₂+(-(11/2)*2+3)*x₃+(-(5/2)*2+2)*x₄+(1*2+3)=0

4-е уравнение: (-(3/2)*1+1)*x₂+(-(11/2)*1+3)*x₃+(-(5/2)*1+4)*x₄+(1*1+3)=0

После преобразований получим следующую систему:

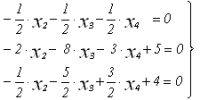
Теперь ведущим элементом будет элемент новой системы А₂₂=-1/2.

Нормирование первого уравнения новой системы: x₂=-x₃-x₄.

2-е уравнение: ((-1)*(-2)+(-8))*x₃+((-1)*(-2)+(-3))*x₄+(0*(-2)+5)=0

3-е уравнение: ((-1)*(-1/2)+(-5/2))*x₃+((-1)*(-1/2)+3/2)*x₄+(0*(-1/2)+4=0

В результате формируется следующая система уравнений:

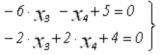
Выбираем снова ведущий элемент А₃₃=-6.

Нормирование 1го уравнения новой системы: x₃=-(1/6)*x₄+(5/6)

Исключаем неизвестую x₃ из оставшегося уравнения: (-(1/6)*(-2)+2)*x₄+((5/6)*2+4)=0

Получим уравнение: (7/3)*x₄+7/3=0.

После нормирования x₄=-1

Обратный ход:

Формирование эквивалентной системы с треугольной матрицей и вычисление неизвестных:

Единственным недостатком является чувствительность к ошибка округления.

Решение систем уравнений методом Гаусса c выбором главного элемента

Большинство распространенных методов решений уравнений являются вариантами метода Гаусса, отличающиеся незначительными нюансами. Метод Гаусса с выбором главного элемента фактически повторяет предыдущий способ за тем исключением, что вместо выбора ведущего элемента на каждом этапе здесь в самом начале определяется главный элемент. Единственным условием выполнения метода является неравенство нулю детерминанта матрицы.

Расширенная прямоугольная матрица коэффициентов СЛУ:

Также как и в обычном методе Гаусса нахождение корней разбивается на два этапа:

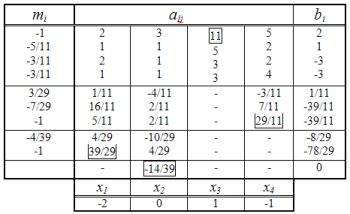
Решение системы уравнений методом Гаусса с выбором главного элемента в табличном представлении.

Прямой ход:

Выбор главного элемента по критерию: A_pq=max|a_ij|, (без учета b_i)

Вычисление множителей m_i=-(a_ij)/(A_pq)

Исключение переменной, соответствующей главному элементу: [строка]_i+[главная строка]*m_i

Таким образом, новая матрица будет на порядок меньше исходной. Иттерационно повторяя аналогичные действия формируем последовательность матриц. В конечном итоге завершающей будет матрица строка.

Обратный ход:

Обратный ход метода заключается в:

1) Объединение главных строк в систему

2) Вычисление x_i

Пример решения системы уравний методом Гаусса с выбором главного элемента можно разобрать по таблице. В отличие от просого метода Гаусса данный способ менее чувствителен к ошибкам округлений.

Метод Гаусса-Жордана для решения системы уравнений

Метод Гаусса-Жордана является еще одной вариацией метода Гаусса для решений систем уравнений. Его отличием является отсутствие обратного хода, но при этом количество действий, выполняемых для решения системы увеличивается. Рассмотрим следующую систему уравнений 3-го порядка:

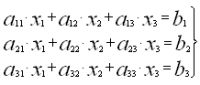
Первым этапом производится нормирование первого уравнения, далее исключается переменная x₁. Отличием является то, что выражение для x_kподставляется во все уравнения кроме k-го (с ведущим элементом). Далее действия повторяются и исключается вторая переменная, а затем и третья.

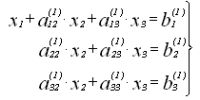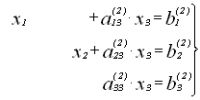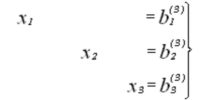Нормирование 1-го уравнения исключение x1	Нормирование 2-го уравнения исключение x2	Нормирование 3-го уравнения исключение x3

Достоинством метода Гаусса-Жордана является простота программирования за счет отсутствия обратного хода.

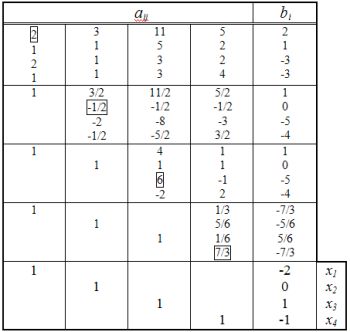
Табличное представление решения системы уравний методом Гаусса-Жордана.

Скачать:

Метод Гаусса для решения системы уравнений - Решение системы линейных уравнений методом Гаусса в Паскале. Исходные данные в файле.

Обратная матрица методом Гаусса - Вычислить обратную матрицу способом Гаусса в turbo pascal. Исходные данные в файле.

Определитель методом Гаусса - Вычисление детерминанта методом Гаусса в Турбо Паскале. Исходные данные в файле.

Решение интеграла методом Гаусса - Вычислить определенный интеграл, используя квадратурную формулу Гаусса. Оценить погрешность квадратурной формулы.

Решение системы уравнений методом Гаусса - Нахождение корней уравнений методом Гаусса в среде Турбо Паскаль.